A new class of chikku kOlams

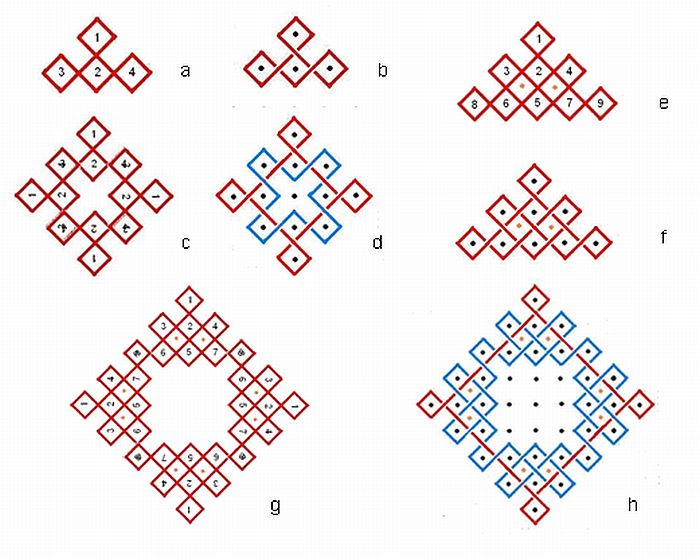
Yesterday, while studying carefully one of the rangOlis displayed, an idea struck me and the result is the possibility of an entirely new class of rangOlis. I will explain the basic principles in this blog and later on give a few more examples in the regular uploads. Let us take a small square with horizontal and vertical lines. Let us rotate it by 45 degrees and let us place such a square and call it 1 (Fig. a). Below 1, let us place another similar square so that the corners touch and let us call it 2. By the side of 2 we place 3 on the left and 4 four on the right. Thus we have a right angled triangle of four squares 1, 2, 3 and 4. The lines connecting these is a single line as shown in Fig. b. Let us take this triangular entity of four squares and rotate it by 90, 180 and 270 degrees and place them together so that the corner squares 3 and 4 coincide. This is shown Fig. c. This has two lines as shown in Fig d. This is a very familiar rangOli, a quickie everyone had drawn sometime or other. Not much new here. I always wondered how the next pattern will look like in this series. Let us go to Fig. e. This has nine squares from 1 to 9 as shown placed one below the other in three rows so that a right angled triangle results. The resultant figure has one line as shown in Fig f. This figure is rotated by 90, 180 and 270 degrees and placed as shown in Fig. g with the corner squares 8 and 9 overlapping. This figure too has two lines as shown in Fig. h, but more elaborate than the simple quickie of Fig. d. In this way we can get more complicated patterns, all having only two lines. The symmetry for this type of arrangement is 422 (90 degree rotations about a vertical axis and four 180 degree rotations in the plane of the figure). There are also other ways in which other different figures may be obtained. Enjoy!

Regards! - mOhana